# 排序 - 插入排序（Insertion Sort）

# 插入排序介绍

直接插入排序 (Straight Insertion Sort) 的基本思想是：把 n 个待排序的元素看成为一个有序表和一个无序表。开始时有序表中只包含 1 个元素，无序表中包含有 n-1 个元素，排序过程中每次从无序表中取出第一个元素，将它插入到有序表中的适当位置，使之成为新的有序表，重复 n-1 次可完成排序过程。

# 插入排序实现

下面选取直接插入排序的一个中间过程对其进行说明。假设 {20,30,40,10,60,50} 中的前 3 个数已经排列过，是有序的了；接下来对 10 进行排列。示意图如下:

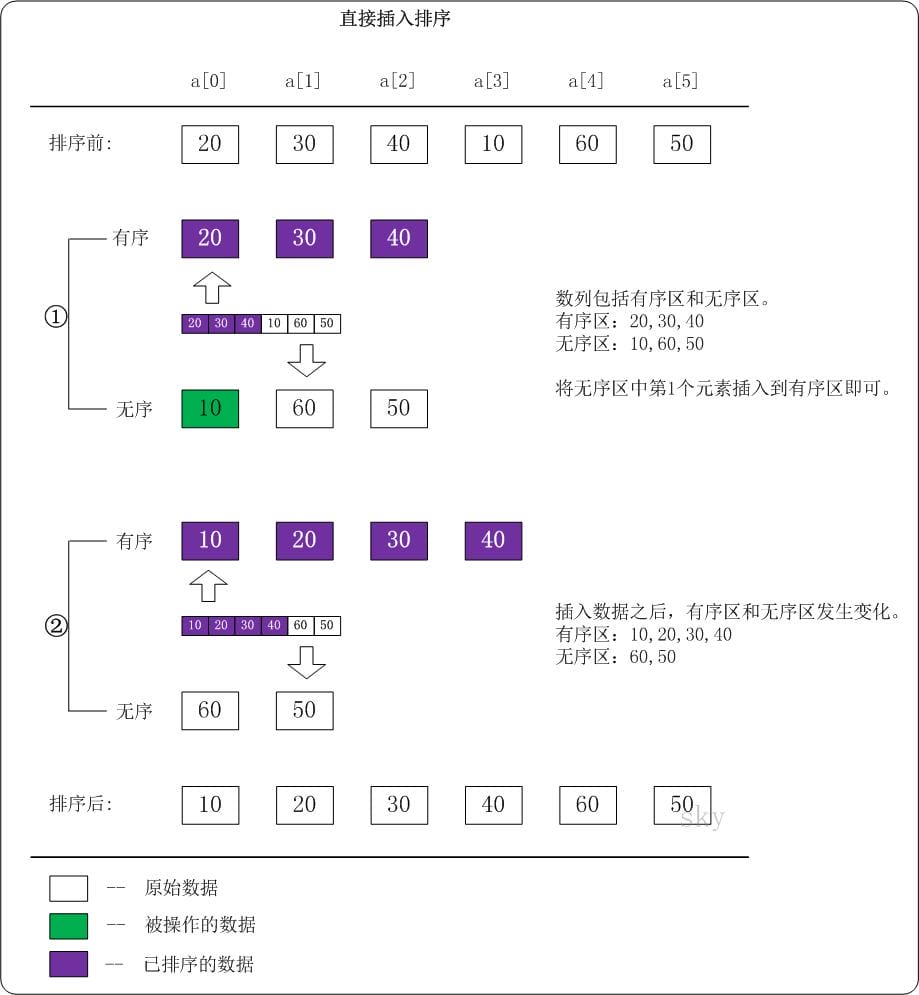
图中将数列分为有序区和无序区。我们需要做的工作只有两个: (1) 取出无序区中的第 1 个数，并找出它在有序区对应的位置。(2) 将无序区的数据插入到有序区；若有必要的话，则对有序区中的相关数据进行移位。

# 插入排序的时间复杂度和稳定性

# 插入排序时间复杂度

直接插入排序的时间复杂度是 O (N2)。

假设被排序的数列中有 N 个数。遍历一趟的时间复杂度是 O (N)，需要遍历多少次呢？N-1！因此，直接插入排序的时间复杂度是 O (N2)。

# 插入排序稳定性

直接插入排序是稳定的算法，它满足稳定算法的定义。

算法稳定性 – 假设在数列中存在 a [i]=a [j]，若在排序之前，a [i] 在 a [j] 前面；并且排序之后，a [i] 仍然在 a [j] 前面。则这个排序算法是稳定的！

	/**
	* 插入排序
	*
	* @author wspstart
	* @create 2023-01-23 21:43
	*/
	public class InsertSort {
	public static void insertSort(int[] a) {
	int i, j, k;

	for (i = 1; i < a.length; i++) {

	// 为 a [i] 在前面的 a [0...i-1] 有序区间中找一个合适的位置
	for (j = i - 1; j >= 0; j--)
	if (a[j] < a[i])
	break;

	// 如找到了一个合适的位置
	if (j != i - 1) {
	// 将比 a [i] 大的数据向后移
	int temp = a[i];
	for (k = i - 1; k > j; k--)
	a[k + 1] = a[k];
	// 将 a [i] 放到正确位置上
	a[k + 1] = temp;
	}
	println(i,a);
	}
	}


	/*
	改进之后代码更加简洁
	*/
	public static void sort(int[] arr) {
	for (int i = 1; i < arr.length; i++) {
	// 记录当前正在待插入的数据
	int temp = arr[i];
	int j;
	// 把大于需要插入的数往后移动，最后不大于 temp 的数就空出来了，j > 0 防止空指针
	for (j = i ; j > 0 && greater(arr[j - 1],temp); j--) {
	arr[j] = arr[j-1];
	}
	// 最后将待插入的元素插入即可
	arr[j] = temp;
	println(i, arr);
	}
	}

	/**
	* 比较 v 元素是否大于 w 元素
	*
	* @param v
	* @param w
	* @return
	*/
	private static boolean greater(int v, int w) {
	return v > w;
	}

	/**
	* 数组元素 i 和 j 交换
	*
	* @param a
	* @param i
	* @param j
	*/
	private static void exch(int[] a, int i, int j) {
	int temp;
	temp = a[i];
	a[i] = a[j];
	a[j] = temp;
	}

	private static void println(int num, int[] a) {
	System.out.println("第" + num + "次循环" + Arrays.toString(a));
	}
	}