B-Tree - 数据结构与算法 - java基础

# 0. 预备知识

二叉树
排序二叉树
AVL 树

# 1. 前言

我们始终假设可以把整个数据结构存储在内存中。可是，如果数据多到内存装不下，这就意味着必须把数据放在磁盘上，显然这些数据结构不再适用。问题在于磁盘的 I/O 速度是远远不如内存访问速度的，然而从一棵树中查找到某个元素，必须从根节点一层层往下找，这每一次查找便是一次 I/O 操作。为了提高性能，就必须要减少查找的次数。如能减少树的高度、增加每个节点中的元素数，便是种有效的解决方案。实现这种想法的一种方法是使用 B 树。

# 2. 相关概念

内部节点（internal）：除根节点和叶子节点之外的节点叫做内部节点。它们即有父节点，也有子节点。
键：B 树中的存储元素是键，是用于指向数据记录的指针。键的值是用于存储真正的数据记录。一个节点中可以拥有多个键。
阶：B 树的阶为最大子节点数量，其比键的数量大 1。我们一般称一个 B 树为 M 阶的 B 树，那么该 B 树最多拥有 M 个子节点，节点中最多拥有 M-1 个键。
**B 树：** 是一种自平衡的树，能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作，都在对数时间内完成。
- 每个节点最多有 M 个子节点；每个内部节点最少有 ⌈M/2⌉ 个子节点（⌈x⌉为向上取整符号）；如果根节点不是叶子节点，那么它至少有两个子节点。
- 具有 N 个子节点的非叶子节点拥有 N-1 个键。
- 非根节点的键值数量在 t - 1 到 2t - 1 中，其中 t = Math.ceil (M/2);
- 所有叶子节点必须处于同一层上。
- B 树的阶是预先定义好的。

# 3. 插入

# 步骤描述：

如果该节点上的元素数未满，则将新元素插入到该节点，并保持节点中元素的顺序。
如果该节点上的元素已满，则需要将该节点平均地分裂成两个节点：
1. 从该节点中的元素和新元素先出一个中位数
2. 小于中位数的元素放到左边节点，大于中位数的元素放到右边节点，中位数做为分隔值。
3. 分隔值被插入到父节点中（增加了树的高度），这可能会导致父节点的分裂，分裂父节点时又可能会使它的父节点分裂，以此类推。如果分裂一直上升到根节点，那么就创建一个新的根节点，它有一个分隔值和两个子节点。（这就是根节点并不像内部节点一样有最少子节点数量限制的原因）

# 图示：

我们通过顺序插入 1 - 17 来学习结点的分裂过程

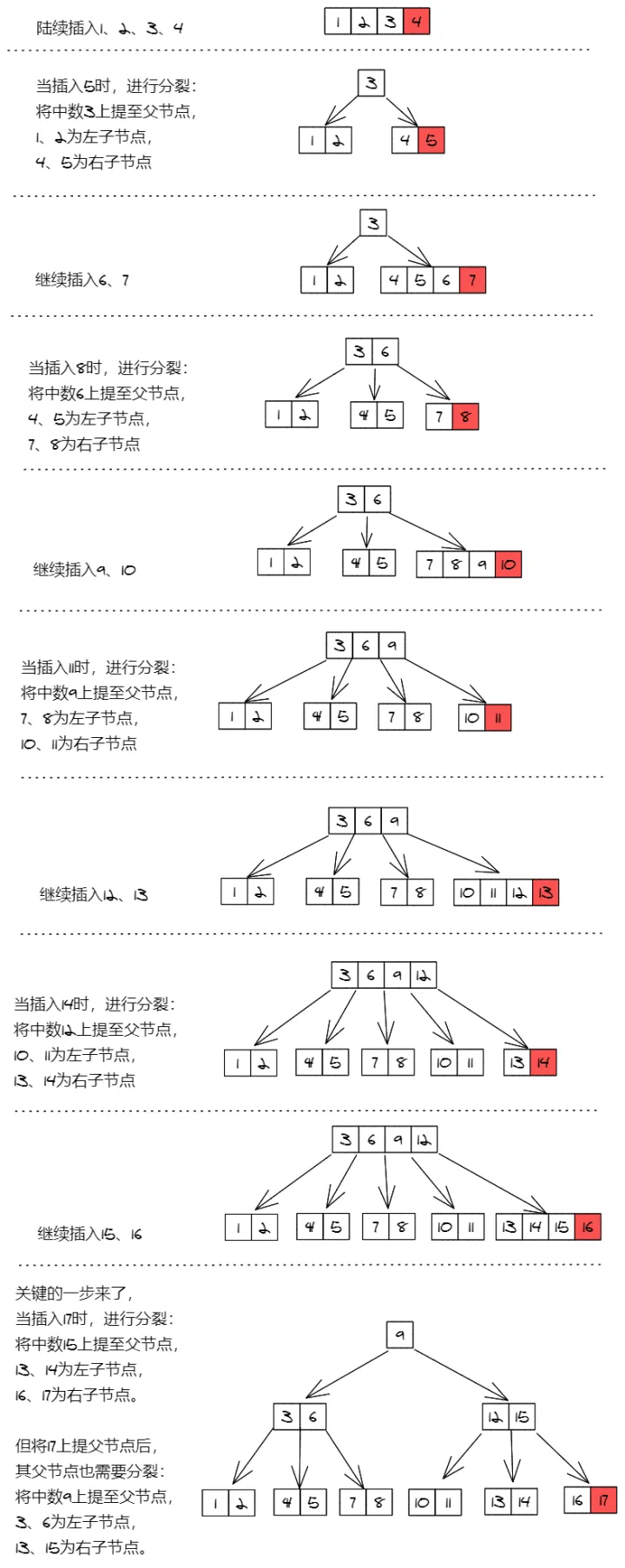看不懂上述题解的，很正常，我第一次也没看懂，看懂了的那么恭喜你可以跳过下面这一小部分了。

# 详细分析

# 情况一：

首先分析一下最简单的情况：分裂根节点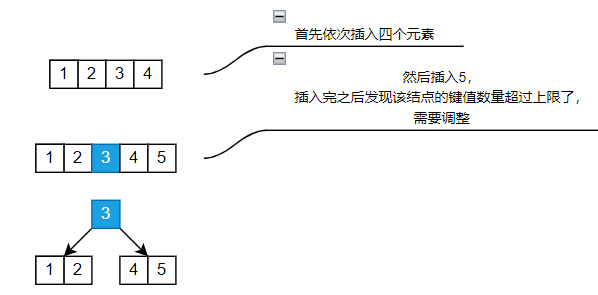** 详细描述：** 由于插入的键值 5，导致结点长度超过了上限。故将其拆分为三部分：左节点、中间结点（即新的根节点）、右节点。左节点的键值为中间键值的左边的所有键值，右节点同理，然后使其中间结点中键值 3 的两侧子结点依次为左节点、右节点。然后将中间结点赋值给根结点，完成分裂。问答：

结点长度超过了上限是什么？
- 由于示例是 5 阶树，所以每个结点最多有 5 - 1 个键值
为什么上移中间结点？
- 因为 B 树是一颗有序的多路平衡查找树，所以为了使其有序且平衡，这里选择中间结点为父结点

# 情况二：

分裂边上的叶子节点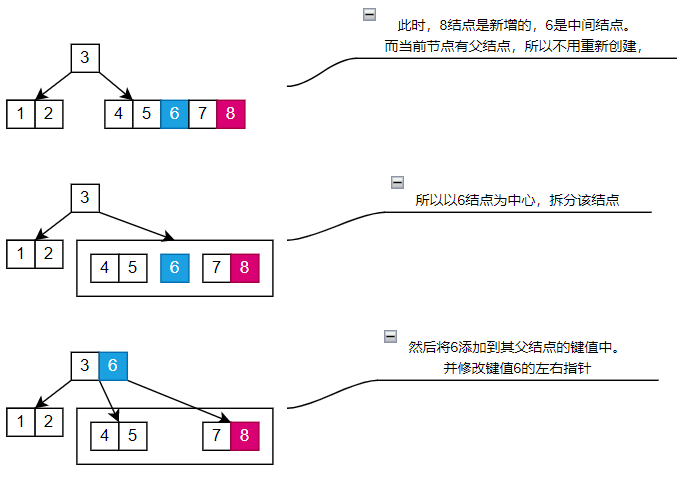

# 情况三：

分裂中间的叶子节点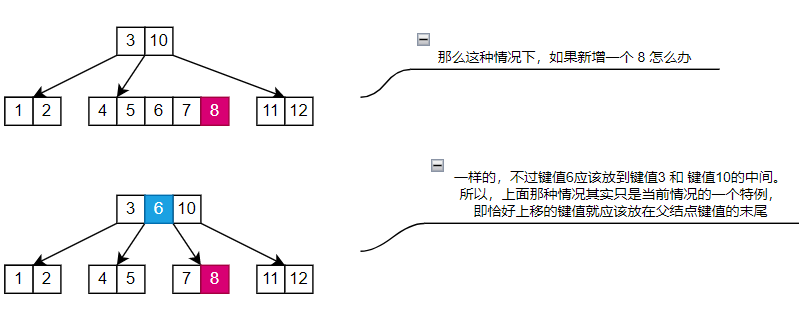这里要注意的就是，在递归的过程中，需要记录一下当前结点在父结点的第几个索引。

# 代码实现

通过上述分析，一个结点需要包含以下元素：

一个存放键值的数组
一个存放子结点引用的数组

还需要分析一下键值和键值两端的引用的索引关系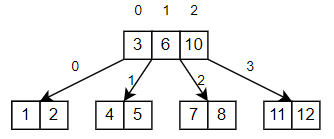由图可见，假设键值的索引为 n，那么其左侧的子结点引用也为 n，右侧的子结点引用为 n + 1Node 类设计好了，还有 BalanceTree 类，BalanceTree 类暂时来说需要的就是该 B 树的阶数，所以构造器应该有一个参数下面就可以进行代码实现了

	package _09_tree;

	import java.util.ArrayList;
	import java.util.Objects;

	/**
	* @description: 实现 B-Tree 的基本功能
	* @author: Ding
	* @version: 1.0
	* @createTime: 2023-01-23 17:32:35
	* @modify:
	*/

	public class BalanceTree<T extends Comparable<T>> {


	private Node head;

	private final int rank;

	public BalanceTree(int rank) {
	this.rank = rank;
	}

	public void add(T key) {
	if (Objects.isNull(head)) {
	head = new Node(null, key, null);
	return;
	}
	doAdd(head, null, -1, key);
	}

	/**
	* 实现向 B 树中插入数据
	* @param node 当前正在进行比较的结点
	* @param father 当前正在进行比较的结点的父结点
	* @param linkIndex 当前结点在父结点的引用列表中的索引位置
	* @param key 需要新增的键值
	*/
	@SuppressWarnings("ConstantConditions")
	private void doAdd(Node node, Node father, int linkIndex, T key) {

	for (int i = 0; i < node.keyList.size(); i++) {
	T nodeKey = node.keyList.get(i);
	int cmp = key.compareTo(nodeKey);

	// 往左
	// key <= nodeKey
	if (cmp <= 0) {

	// 如果是叶子结点
	if (node.isLeaf()) {
	node.keyList.add(i, key);
	node.linkList.add(null);
	}
	else {
	doAdd(node.getLeftNode(i), node, i, key);
	}
	break;
	}

	// 如果是最后一个键值，那么就需要判断最后一个键值的右子结点
	if (i == node.keyList.size() - 1) {
	if (node.isLeaf()) {
	node.keyList.add(i + 1, key);
	node.linkList.add(null);
	} else {
	doAdd(node.getRightNode(i), node, i + 1, key);
	}
	break;
	}
	}

	// 如果当前结点超出了上限，需要调整
	if (node.isOverflow()) {
	// 分裂
	if (Objects.isNull(father)) {
	// 当前节点是根结点，需要新建根结点
	int middleIndex = node.keyList.size() / 2;
	// 初始化三个结点
	Node left = new Node();
	Node right = new Node();
	Node newHead = new Node();
	// 根据中间键值拆分
	for (int i = 0; i < node.keyList.size(); i++) {

	if (i < middleIndex) {
	left.keyList.add(node.keyList.get(i));
	left.linkList.add(node.getLeftNode(i));
	} else if (i > middleIndex) {
	right.keyList.add(node.keyList.get(i));
	right.linkList.add(node.getRightNode(i));
	} else {
	left.linkList.add(node.getLeftNode(i));
	newHead.keyList.add(node.keyList.get(i));
	right.linkList.add(node.getRightNode(i));
	}
	}
	// 完善新的根节点
	newHead.linkList.add(left);
	newHead.linkList.add(right);
	this.head = newHead;
	} else {
	// 获取中间键值的索引
	int middleIndex = node.keyList.size() / 2;
	// 初始化左右子结点，此处由于已经有了父结点，所以无需重复初始化父结点
	Node left = new Node();
	Node right = new Node();
	// 根据中间键值进行拆分
	for (int i = 0; i < node.keyList.size(); i++) {
	if (i < middleIndex) {
	left.keyList.add(node.keyList.get(i));
	left.linkList.add(node.getLeftNode(i));
	} else if (i > middleIndex) {
	right.keyList.add(node.keyList.get(i));
	right.linkList.add(node.getRightNode(i));
	} else {
	left.linkList.add(node.getLeftNode(i));
	right.linkList.add(node.getRightNode(i));
	}
	}
	// 将中间键值添加到父结点的键值列表中
	father.keyList.add(linkIndex, node.keyList.get(middleIndex));
	// 修改引用列表
	father.linkList.set(linkIndex, left);
	father.linkList.add(linkIndex + 1, right);

	}
	}
	}


	@Override
	public String toString() {
	return middleOrder();
	}

	private String middleOrder() {
	StringBuilder stringBuilder = new StringBuilder("[");
	doMiddleOrder(head, stringBuilder);
	if (stringBuilder.toString().endsWith(", ")) {
	stringBuilder.delete(stringBuilder.length() - 2, stringBuilder.length());
	}
	return stringBuilder.append("]").toString();
	}

	private void doMiddleOrder(Node node, StringBuilder stringBuilder) {
	if (Objects.isNull(node)) {
	return;
	}
	stringBuilder.append("[");
	// 遍历根节点索引
	for (int i = 0; i < node.linkList.size(); i++) {
	// 先往树的深处遍历，找到最小的结点
	doMiddleOrder(node.linkList.get(i), stringBuilder);
	// 然后添加元素
	if (i < node.keyList.size()) {
	stringBuilder.append(node.keyList.get(i)).append(", ");
	}
	}
	if (stringBuilder.length() > 1) {
	stringBuilder.delete(stringBuilder.length() - 2, stringBuilder.length());
	}
	stringBuilder.append("], ");
	}

	private class Node {

	/**
	* 存放当前结点的所有键值。
	* 键两端对子结点的引用存放在 {@link #linkList} 中，假设键的索引为 n，那么其左子结点引用的索引为 2n，右子结点的引用为 2n + 1
	*/
	ArrayList<T> keyList;

	/**
	* 存放当前结点的子结点引用。
	*/
	ArrayList<Node> linkList;

	int keyListMaxLength = rank - 1;

	int linkListMaxLength = rank;

	public Node() {
	keyList = new ArrayList<>();
	linkList = new ArrayList<>();
	}

	public Node(Node leftNode, T key, Node rightNode) {
	this();
	keyList.add(key);
	linkList.add(leftNode);
	linkList.add(rightNode);
	}

	/**
	* @param keyIndex 键的索引
	* @return 返回当前结点中，索引为 keyIndex 的左子结点
	*/
	public Node getLeftNode(int keyIndex) {
	if (keyIndex < this.keyList.size()) {
	return linkList.get(keyIndex);
	}
	return null;
	}

	/**
	* @param keyIndex 键的索引
	* @return 返回当前结点中，索引为 keyIndex 的左子结点
	*/
	public Node getRightNode(int keyIndex) {
	if (keyIndex < this.keyList.size()) {
	return linkList.get(keyIndex + 1);
	}
	return null;
	}

	/**
	* @return 返回 true 表示当前结点已经满了，即键的数量为 {@link #rank} - 1
	*/
	public boolean isFull() {
	return keyList.size() >= keyListMaxLength;
	}

	/**
	* @return 返回 true 表示当前结点是叶子节点
	*/
	public boolean isLeaf() {
	return linkList.stream().allMatch(Objects::isNull);
	}

	/**
	* @return 返回 true 表示当前结点已经溢出了，需要调整
	*/
	public boolean isOverflow() {
	return keyList.size() > keyListMaxLength;
	}

	/**
	* @return 返回当前结点的中间键值
	*/
	public T getMiddleKey() {
	return keyList.get(keyList.size() / 2);
	}
	}

	}

# 4. 删除

# 步骤描述：

删除叶子节点中的关键字
- 搜索要删除的关键字，然后将其删除
- 判断结点还是否符合条件（即结点的关键字个数是否在 [t - 1, 2t - 1]
  - 若符合条件则跳过
  - 若不符合条件则向其兄弟节点借关键字。即将其父节点关键字下移至当前节点，将兄弟节点中关键字上移至父节点（若是左节点，上移最大关键字；若是右节点，上移最小关键字）
    - 若兄弟节点也达到下限，则合并兄弟节点与分割键。
删除内部节点中的关键字
- 删除内部节点的关键字可转换为删除叶子节点的关键字。即首先判断是否为叶子节点，否：则将子结点的关键字上移并覆盖当前的待删除关键字，然后继续递归删除子结点中上移的那个关键字。然后继续判断。。。

# 图示：

下图是一个 5 阶 B 树，我们通过删除 15、14、17、5 四个键，来观察删除过程（基本涵盖所有情况）。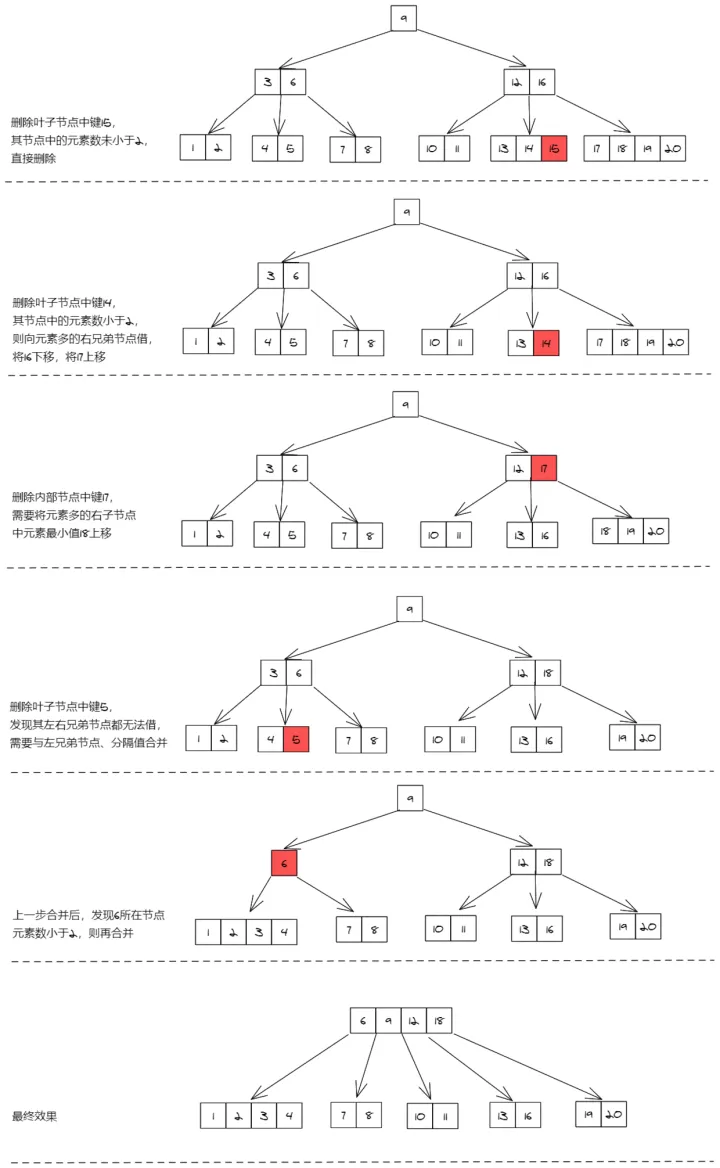

# 详细描述：

详见代码

# 代码实现：（包括前面的插入代码）

	package _09_tree;

	import java.util.ArrayList;
	import java.util.Objects;

	/**
	* @description: 实现 B-Tree 的基本功能
	* @author: Ding
	* @version: 1.0
	* @createTime: 2023-01-23 17:32:35
	* @modify:
	*/

	public class BalanceTree<T extends Comparable<T>> {


	private Node head;

	private final int rank;

	public BalanceTree(int rank) {
	this.rank = rank;
	}

	public void add(T key) {
	if (Objects.isNull(head)) {
	head = new Node(null, key, null);
	return;
	}
	doAdd(head, null, -1, key);
	}

	/**
	* 实现向 B 树中插入数据
	* @param node 当前正在进行比较的结点
	* @param father 当前正在进行比较的结点的父结点
	* @param linkIndex 当前结点在父结点的引用列表中的索引位置
	* @param key 需要新增的键值
	*/
	@SuppressWarnings("ConstantConditions")
	private void doAdd(Node node, Node father, int linkIndex, T key) {

	for (int i = 0; i < node.keyList.size(); i++) {
	T nodeKey = node.keyList.get(i);
	int cmp = key.compareTo(nodeKey);

	// 往左
	// key <= nodeKey
	if (cmp <= 0) {

	// 如果是叶子结点
	if (node.isLeaf()) {
	node.keyList.add(i, key);
	node.linkList.add(null);
	}
	else {
	doAdd(node.getLeftNode(i), node, i, key);
	}
	break;
	}

	// 如果是最后一个键值，那么就需要判断最后一个键值的右子结点
	if (i == node.keyList.size() - 1) {
	if (node.isLeaf()) {
	node.keyList.add(i + 1, key);
	node.linkList.add(null);
	} else {
	doAdd(node.getRightNode(i), node, i + 1, key);
	}
	break;
	}
	}

	// 如果当前结点超出了上限，需要调整
	if (node.isUpOverflow()) {
	// 分裂
	if (Objects.isNull(father)) {
	// 当前节点是根结点，需要新建根结点
	int middleIndex = node.keyList.size() / 2;
	// 初始化三个结点
	Node left = new Node();
	Node right = new Node();
	Node newHead = new Node();
	// 根据中间键值拆分
	for (int i = 0; i < node.keyList.size(); i++) {

	if (i < middleIndex) {
	left.keyList.add(node.keyList.get(i));
	left.linkList.add(node.getLeftNode(i));
	} else if (i > middleIndex) {
	right.keyList.add(node.keyList.get(i));
	right.linkList.add(node.getRightNode(i));
	} else {
	left.linkList.add(node.getLeftNode(i));
	newHead.keyList.add(node.keyList.get(i));
	right.linkList.add(node.getRightNode(i));
	}
	}
	// 完善新的根节点
	newHead.linkList.add(left);
	newHead.linkList.add(right);
	this.head = newHead;
	} else {
	// 获取中间键值的索引
	int middleIndex = node.keyList.size() / 2;
	// 初始化左右子结点，此处由于已经有了父结点，所以无需重复初始化父结点
	Node left = new Node();
	Node right = new Node();
	// 根据中间键值进行拆分
	for (int i = 0; i < node.keyList.size(); i++) {
	if (i < middleIndex) {
	left.keyList.add(node.keyList.get(i));
	left.linkList.add(node.getLeftNode(i));
	} else if (i > middleIndex) {
	right.keyList.add(node.keyList.get(i));
	right.linkList.add(node.getRightNode(i));
	} else {
	left.linkList.add(node.getLeftNode(i));
	right.linkList.add(node.getRightNode(i));
	}
	}
	// 将中间键值添加到父结点的键值列表中
	father.keyList.add(linkIndex, node.keyList.get(middleIndex));
	// 修改引用列表
	father.linkList.set(linkIndex, left);
	father.linkList.add(linkIndex + 1, right);

	}
	}
	}

	/**
	* @param key 要删除的关键字
	* @return 返回是否删除成功，当且仅当关键字不存在时返回 false
	*/
	public boolean remove(T key) {
	if (Objects.isNull(key) \|\| Objects.isNull(head)) return false;
	// 进行真正的删除操作
	boolean isSuccesses = doRemove(head, null, -1, key);
	// 判断本次删除之后根节点是否为空
	if (head.keyList.isEmpty()) {
	head = null;
	}
	return isSuccesses;
	}

	@SuppressWarnings("ConstantConditions")
	private boolean doRemove(Node node, Node father, int linkIndex, T key) {
	boolean isSuccesses = false;
	// 循环遍历当前结点中的关键字
	for (int i = 0; i < node.keyList.size(); i++) {
	// 比较大小
	int cmp = key.compareTo(node.keyList.get(i));
	// key < node.keyList.get(i)
	if (cmp < 0) {
	// 往左
	if (node.isLeaf()) {
	// 如果是叶子节点，说明该关键字不存在，故返回 false
	return false;
	} else {
	// 递归删除
	isSuccesses = doRemove(node.getLeftNode(i), node, i, key);
	// 递归删除之后默认
	break;
	}
	// key == node.keyList.get(i)
	} else if (cmp == 0) {
	// 判断是否为叶子节点
	if (node.isLeaf()) {
	// 如果是叶子节点那么就直接删除
	node.keyList.remove(key);
	node.linkList.remove(node.linkList.size() - 1);
	}
	// 如果是非叶子结点，那么就在其子结点找个替罪羊，然后继续递归删除其子结点的替罪羊
	else {
	// 获取其子结点
	Node son = node.linkList.get(i);
	// 获取替罪羊关键字
	// 为什么获取最大的一个？
	// 因为，获取子结点时，是获取的当前关键字左侧的子结点，所以应使用该子结点的最大关键字来当替罪羊
	T scapegoat = son.keyList.get(son.keyList.size() - 1);
	// 使替罪羊关键字覆盖待删除关键字
	node.keyList.set(i, scapegoat);
	// 递归删除替罪羊关键字
	doRemove(son, node, i, scapegoat);
	}
	// 只要有相等的值，那么就一定删除成功
	isSuccesses = true;
	break;
	}
	// 如果是最后一个关键字，那么就需要判断是否需要向最后一个关键字的右子结点进行递归
	if (i == node.keyList.size() - 1) {
	// 如果是叶子节点，并且还未删除
	if (node.isLeaf()) {
	return false;
	} else {
	isSuccesses = doRemove(node.getRightNode(i), node, i + 1, key);
	break;
	}
	}
	}

	if (node.isDownOverflow() && Objects.nonNull(father)) {
	// 向兄弟借
	if (! borrowByBrother(node, father, linkIndex)) {
	// 借不到，就和兄弟合并
	merge(node, father, linkIndex);
	}
	}
	return isSuccesses;
	}

	/**
	*
	* @param node 要合并的结点
	* @param father 要合并的结点的父结点
	* @param linkIndex 要合并的结点在父结点的引用列表中的索引
	*/
	private void merge(Node node, Node father, int linkIndex) {
	// 合并后的新节点
	Node newNode = new Node();
	// 如果是第一个结点，那么就与其右兄弟合并
	if (linkIndex == 0) {
	// 获取右兄弟结点
	Node rightBrotherNode = father.linkList.get(linkIndex + 1);
	// 合并关键字
	newNode.keyList.addAll(node.keyList);
	newNode.keyList.add(father.keyList.remove(linkIndex));
	newNode.keyList.addAll(rightBrotherNode.keyList);
	// 合并引用
	newNode.linkList.addAll(node.linkList);
	newNode.linkList.addAll(rightBrotherNode.linkList);
	// 修改父结点的引用
	father.linkList.set(linkIndex, newNode);
	father.linkList.remove(linkIndex + 1);

	}
	// 如果不是第一个结点，那么必有左兄弟，那就和左兄弟合并
	else {
	// 获取左兄弟结点
	Node leftBrotherNode = father.linkList.get(linkIndex - 1);
	// 合并关键字
	newNode.keyList.addAll(leftBrotherNode.keyList);
	newNode.keyList.add(father.keyList.remove(linkIndex - 1));
	newNode.keyList.addAll(node.keyList);
	// 合并引用
	newNode.linkList.addAll(leftBrotherNode.linkList);
	newNode.linkList.addAll(node.linkList);
	// 修改父结点的引用
	father.linkList.set(linkIndex, newNode);
	father.linkList.remove(linkIndex - 1);
	}
	// 如果此次合并，向根节点借了关键字，导致了根节点关键字个数为 0，那么当前新节点就是根节点
	if (head.keyList.isEmpty()) {
	head = newNode;
	}
	}

	/**
	*
	* @param node 要向兄弟借关键字的结点
	* @param father 要向兄弟借关键字的结点的父结点
	* @param linkIndex 要向兄弟借关键字的结点在父结点的引用列表中的索引
	* @return 返回是否借到关键字
	*/
	private boolean borrowByBrother(Node node, Node father, int linkIndex) {
	// 获取左侧兄弟结点
	Node leftBrotherNode = father.linkList.get(Math.max(linkIndex - 1, 0));
	// 判断是否可以借到关键字
	if (Objects.nonNull(leftBrotherNode) && leftBrotherNode.canBorrow()) {
	// 可以借到的话，先获取关键字（同时删除左侧结点的被借出去的关键字）
	T leftBrotherKey = leftBrotherNode.keyList.remove(leftBrotherNode.keyList.size() - 1);
	// 将当前结点对应的父结点中的关键字到关键字列表中
	node.keyList.add(0, father.keyList.get(linkIndex - 1));
	// 修改当前结点对应的父结点中的关键字为左兄弟借出去的结点
	father.keyList.set(linkIndex - 1, leftBrotherKey);
	return true;
	}
	// 类似上面
	Node rightBrotherNode = father.linkList.get(Math.min(linkIndex + 1, father.linkList.size() - 1));
	if (Objects.nonNull(rightBrotherNode) && rightBrotherNode.canBorrow()) {
	T rightBrotherKey = rightBrotherNode.keyList.remove(0);
	node.keyList.add(father.keyList.get(linkIndex));
	father.keyList.set(linkIndex, rightBrotherKey);
	return true;
	}
	return false;
	}


	@Override
	public String toString() {
	return middleOrder();
	}

	private String middleOrder() {
	StringBuilder stringBuilder = new StringBuilder("[");
	doMiddleOrder(head, stringBuilder);
	if (stringBuilder.toString().endsWith(", ")) {
	stringBuilder.delete(stringBuilder.length() - 2, stringBuilder.length());
	}
	return stringBuilder.append("]").toString();
	}

	private void doMiddleOrder(Node node, StringBuilder stringBuilder) {
	if (Objects.isNull(node)) {
	return;
	}
	stringBuilder.append("[");
	// 遍历根节点索引
	for (int i = 0; i < node.linkList.size(); i++) {
	// 先往树的深处遍历，找到最小的结点
	doMiddleOrder(node.linkList.get(i), stringBuilder);
	// 然后添加元素
	if (i < node.keyList.size()) {
	stringBuilder.append(node.keyList.get(i)).append(", ");
	}
	}
	if (stringBuilder.length() > 1) {
	stringBuilder.delete(stringBuilder.length() - 2, stringBuilder.length());
	}
	stringBuilder.append("], ");
	}

	private class Node {

	/**
	* 存放当前结点的所有键值。
	* 键两端对子结点的引用存放在 {@link #linkList} 中，假设键的索引为 n，那么其左子结点引用的索引为 2n，右子结点的引用为 2n + 1
	*/
	ArrayList<T> keyList;

	/**
	* 存放当前结点的子结点引用。
	*/
	ArrayList<Node> linkList;

	int keyListMaxLength = rank - 1;

	int keyListMinLength = rank >> 1;

	int linkListMaxLength = rank;

	public Node() {
	keyList = new ArrayList<>();
	linkList = new ArrayList<>();
	}

	public Node(Node leftNode, T key, Node rightNode) {
	this();
	keyList.add(key);
	linkList.add(leftNode);
	linkList.add(rightNode);
	}

	/**
	* @param keyIndex 键的索引
	* @return 返回当前结点中，索引为 keyIndex 的左子结点
	*/
	public Node getLeftNode(int keyIndex) {
	if (keyIndex < this.keyList.size()) {
	return linkList.get(keyIndex);
	}
	return null;
	}

	/**
	* @param keyIndex 键的索引
	* @return 返回当前结点中，索引为 keyIndex 的左子结点
	*/
	public Node getRightNode(int keyIndex) {
	if (keyIndex < this.keyList.size()) {
	return linkList.get(keyIndex + 1);
	}
	return null;
	}

	/**
	* @return 返回 true 表示当前结点已经满了，即键的数量为 {@link #rank} - 1
	*/
	public boolean isFull() {
	return keyList.size() >= keyListMaxLength;
	}

	/**
	* @return 返回 true 表示当前结点是叶子节点
	*/
	public boolean isLeaf() {
	return linkList.stream().allMatch(Objects::isNull);
	}

	/**
	* @return 返回 true 表示当前结点已经向上溢出了
	*/
	public boolean isUpOverflow() {
	return keyList.size() > keyListMaxLength;
	}

	/**
	* @return 返回 true 表示当前节点已经向下溢出了
	*/
	public boolean isDownOverflow() {
	return keyList.size() < keyListMinLength;
	}

	/**
	* @return 返回当前结点的中间键值
	*/
	public T getMiddleKey() {
	return keyList.get(keyList.size() / 2);
	}

	/**
	* @return 返回 true 表示能够出借一个键值
	*/
	public boolean canBorrow() {
	return keyList.size() - 1 >= keyListMinLength;
	}
	}

	}

# 5. 查找

搜索就类似其 toString 中的中序遍历，就不赘述了

# 【参考资料】

『数据结构与算法』B 树图文详解（含完整代码）终于把 B 树搞明白了 (一)_B 树的引入，为什么会有 B 树_哔哩哔哩_bilibili1. mysql 面试题 - 深入理解 B + 树原理_哔哩哔哩_bilibili

# 0. 预备知识

# 1. 前言

# 2. 相关概念

# 3. 插入

# 步骤描述：

# 图示：

# 详细分析

# 情况一：

# 情况二：

# 情况三：

# 代码实现

# 4. 删除

# 步骤描述：

# 图示：

# 详细描述：

# 代码实现：（包括前面的插入代码）

# 5. 查找

# 【参考资料】

RB-Tree

JDK 的动态代理之源码解析