# 0. 预备知识
- AVL 树
- 2-3-4 树
# 1. 前言
红黑树（Red Black Tree） 是一种自平衡二叉查找树。红黑树是在 1972 年由 Rudolf Bayer 发明的，当时被称为平衡二叉 B 树（symmetric binary B-trees）。后来，在 1978 年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的 “红黑树”。红黑树是一种平衡二叉查找树的变体，它的左右子树高差有可能大于 1，所以红黑树不是严格意义上的平衡二叉树（AVL），但 对之进行平衡的代价较低， 其平均统计性能要强于 AVL 。
作者说：正是因为 AVL 树的平衡条件过于严格，导致频繁修改数据时会导致大量的旋转操作，从而影响性能。而红黑树利用改变结点颜色达到了减少了旋转操作次数，所以其平均统计性能要强于 AVL。
# 2. 红黑树特征
- 结点是红色或黑色。
- 根结点是黑色。
- 所有叶子都是黑色。（叶子是 NIL 结点）
- 每个红色结点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色结点）
- 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。
关于特征原理解释，详见：1 - 红黑树前置知识 - 二叉排序树常见操作详解_哔哩哔哩_bilibili 由上视频可知，一颗红黑树对应着唯一一颗 2-3-4 树，一颗 2-3-4 树对应多颗红黑树。两者结点转换关系如下：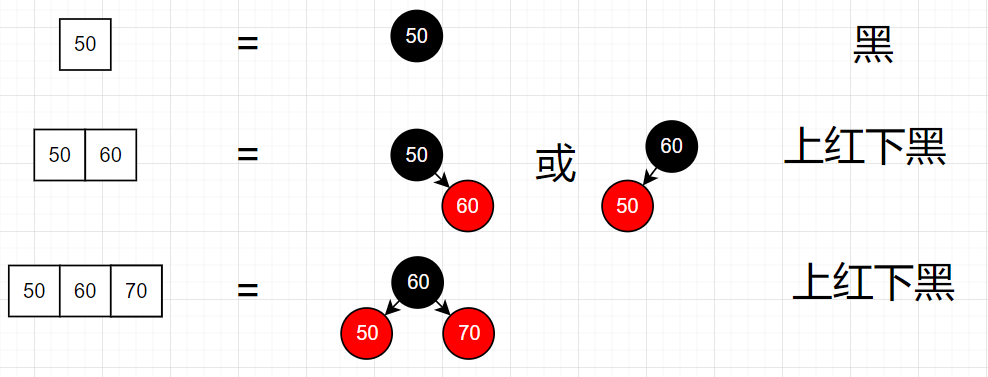
# 3. 插入（结合 2-3-4 Tree 进行理解）
这里我们通过顺序插入 ** {50, 60, 70, 80, 90, 100} ** 来进行理解下图都按照以下结构：
# 3.1 插入 50
# 3.2 插入 60
# 3.3 插入 70
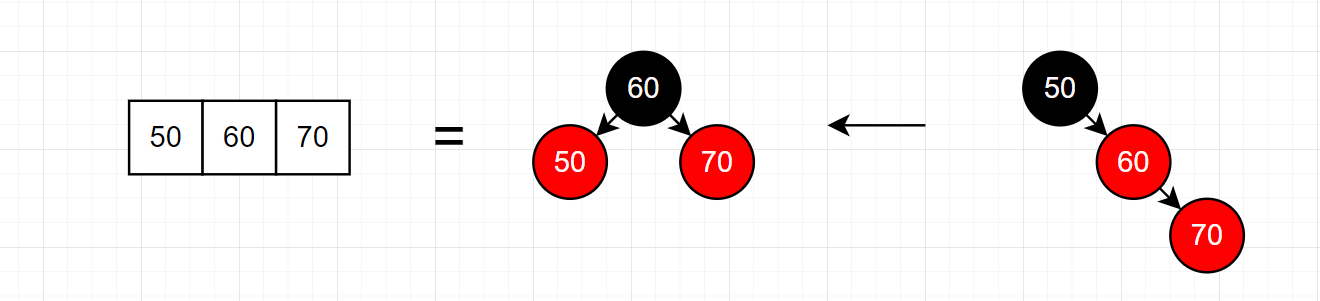此时插入 70 后需要左旋。
# 3.4 插入 80
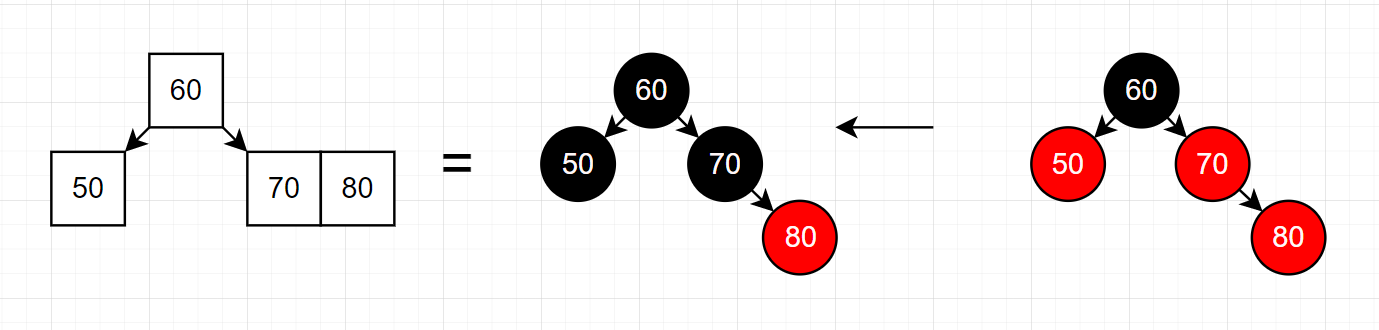此时直接改变颜色即可
# 3.5 插入 90
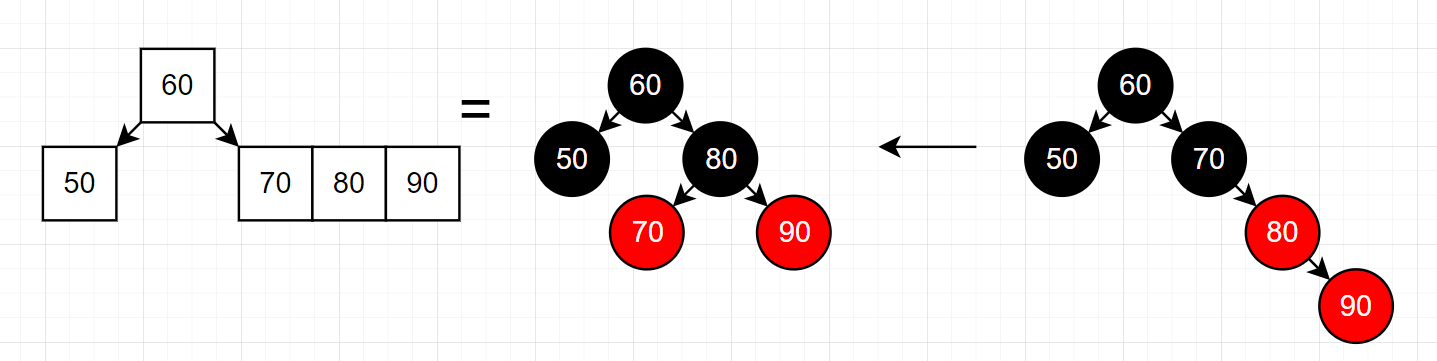需要左旋
# 3.6 插入 100
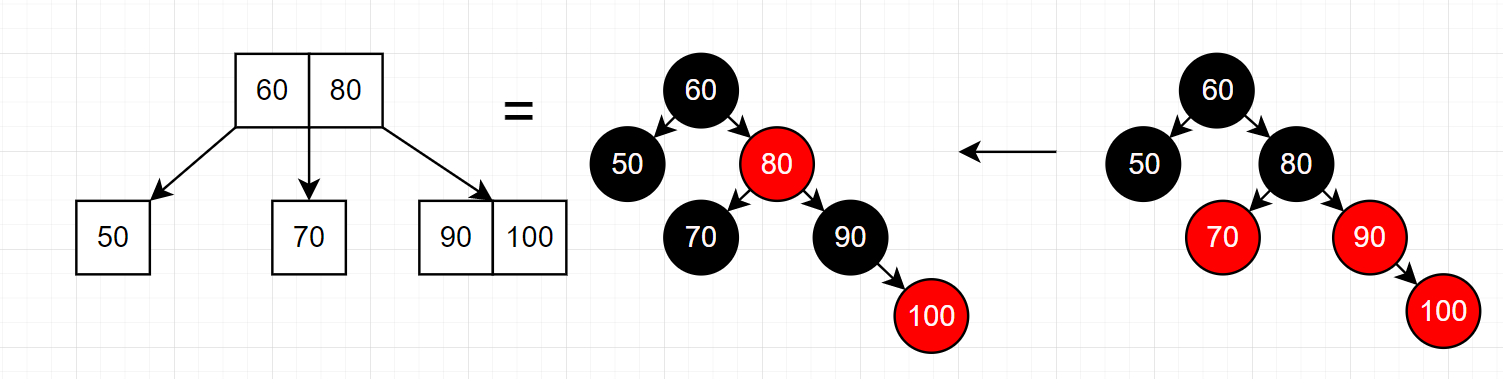此时，若使用 AVL 树存储数据，那么就要进行一次左旋，而红黑树利用改变结点颜色避免了一次左旋，树也差不多是平衡的。
# 结论
观察上述插入过程，可以发现：
# 插入过程
- 插入的结点始终是红色（根节点除外）
- 若父结点的兄弟结点存在，则改变颜色即可，无需旋转
- 例如插入 80、100 时
- 若父结点的兄弟结点不存在，则需要根据树的偏移情况进行旋转，旋转完成之后再修改颜色
- 例如插入 70、90 时
# 颜色改变
分两种情况：
旋转通常只涉及三结点，在 AVL 中，我们会在三结点的上结点发现树不平衡，需要旋转，而在红黑树中，我们会在三结点的中结点发现需要旋转。所以下面两点中的 当前节点 指的是旋转三结点的中结点
- 旋转后改变颜色
- 三结点通过 L、R、LR、RL 旋转完成之后都是 一上二下式，所以旋转完成之后修改父结点为黑色，下方两个子结点为 红色即可。
- 不旋转，直接改变颜色
- 这种情况是父结点有兄弟结点，则直接将父结点设为红色（注意父结点是根节点的情况），当前结点和兄弟结点设为黑色即可。
